Part 3/6 - Calculate elevation difference and distance between points, and visualize the elevation profile with Python
Last week you learned how to visualize a GPX Strava route with Python and Folium, and the week before you’ve seen how to analyze and parse Strava GPX routes. Today we’ll take things to the next level by calculating the elevation difference and distance between data points. We’ll also visualize the elevation profile of a route and compare it to the one generated by Strava.
We have a lot of things to cover, so let’s dive straight in. First, we’ll load in the dataset and calculate the elevation difference.
Don’t feel like reading? Watch my video instead:
You can download the source code on GitHub.
How to Read a Strava Route Dataset
We won’t bother with GPX files today, as we already have route data points extracted to a CSV file. To start, we’ll import a couple of libraries - Numpy, Pandas, and Haversine (pip install haversine) - but also Matplotlib for visualization later on:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import haversine as hs
plt.rcParams['figure.figsize'] = (16, 6)
plt.rcParams['axes.spines.top'] = False
plt.rcParams['axes.spines.right'] = False
From here, load the route dataset:
route_df = pd.read_csv('../data/route_df.csv')
route_df.head()
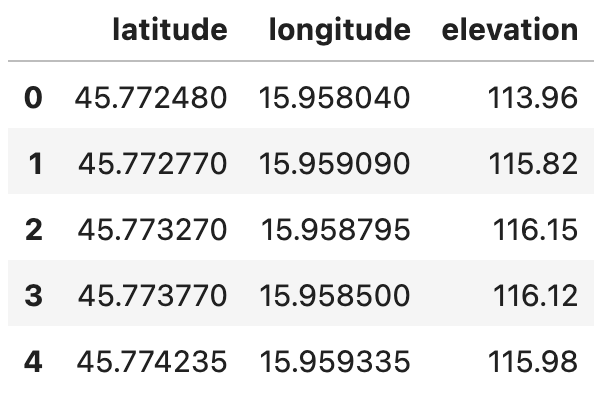
Image 1 - Strava route dataset (image by author)
There are 835 data points in total, and we have elevation data for each. How can we get the elevation difference between points? Let’s cover that next.
How to Calculate Elevation Difference From a Strava Route
You can use the diff() function from Pandas to calculate the difference between row N+1 and N. If you apply it to the elevation column, you’ll get the elevation difference between individual points. The first differenced value will be NaN, but that’s expected, as there’s no data point before it.
Use the code snippet below to calculate the elevation difference and store it into a separate column:
route_df['elevation_diff'] = route_df['elevation'].diff()
route_df.head()
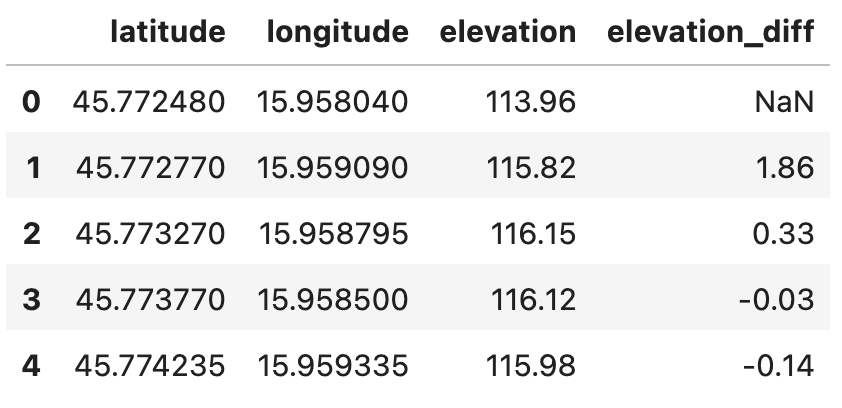
Image 2 - Route dataset with elevation difference (image by author)
In plain English, the second point sits 1.86 meters above the first point. But what is the actual distance between points? 1.86 meters of elevation is extremely difficult to ride over 10 meters but fairly easy over a 100.
You’ll calculate the distance between points next.
How to Calculate Distance Between Points in a Strava Route
Calculating distances between data points on a cycling route is tricky. Probably the best approach is to use some of Google’s mapping APIs - but these aren’t free and usually work well on road only. This is a limiting factor for mountain bike trails. Also, making close to a thousand API requests would take a couple of minutes at least.
The best free and fast option is to use the Haversine distance. It calculates a great circle distance between two points on a sphere given their latitudes and longitudes. For deeper dive into the theory and mathematics, feel free to read the official Wikipedia article.
Our GPX Strava route measures 36,4 kilometers and has 835 data points. On average, that’s around 43,6 meters between points. Strava routes look extra smooth, so I’d expect to see fewer data points on straight roads and more points on trails, as they have a lot of sharp turns. It’s reasonable to expect that Haversine distance will be a bit off, but hopefully not much.
First, let’s define a function to calculate the Haversine distance. It takes in two latitude and longitude combinations and returns the distance between these in meters:
def haversine_distance(lat1, lon1, lat2, lon2) -> float:
distance = hs.haversine(
point1=(lat1, lon1),
point2=(lat2, lon2),
unit=hs.Unit.METERS
)
return np.round(distance, 2)
The code snippet below prints the distance between the first and the second point in the dataset:
haversine_distance(
lat1=route_df.iloc[0]['latitude'],
lon1=route_df.iloc[0]['longitude'],
lat2=route_df.iloc[1]['latitude'],
lon2=route_df.iloc[1]['longitude']
)
You should see 87.59 printed to the console. There’s no way to verify it through Strava, but let’s hope it’s accurate.
We’ll now calculate the distances between all data points. The code snippet below does that, and also skips the first row as there’s no data point before it. When done, the distances are stored in a new column:
distances = [np.nan]
for i in range(len(route_df)):
if i == 0:
continue
else:
distances.append(haversine_distance(
lat1=route_df.iloc[i - 1]['latitude'],
lon1=route_df.iloc[i - 1]['longitude'],
lat2=route_df.iloc[i]['latitude'],
lon2=route_df.iloc[i]['longitude']
))
route_df['distance'] = distances
route_df.head()
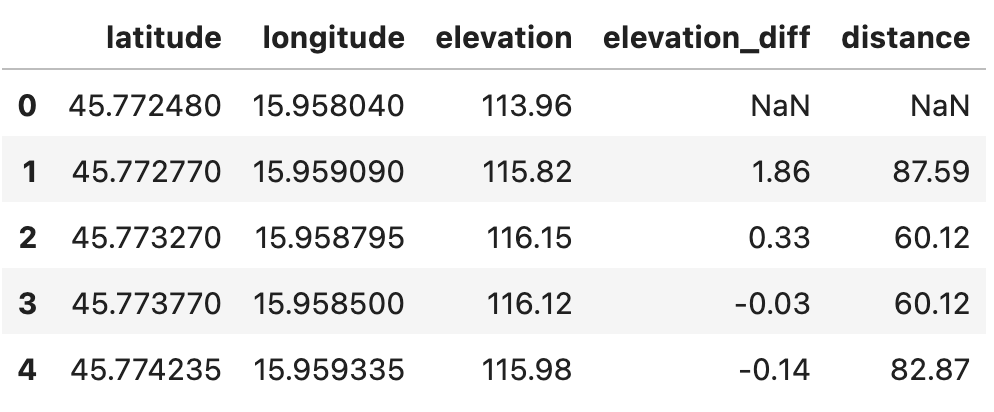
Image 3 - Route dataset with the distance between data points (image by author)
These new columns are interesting to explore. For example, we can calculate the total elevation gain of a route. How? By subsetting the dataset so only rows with positive elevation_diff are kept, and then summing the mentioned column:
route_df[route_df['elevation_diff'] >= 0]['elevation_diff'].sum()

Image 4 - Total elevation gain of the Strava route (image by author)
The number is a bit off, as the official Strava route states there’s 288 meters of elevation.
Let’s check the total distance next. The route is 36,4 kilometers long according to Strava. We’ll sum the distance column and compare the results:
route_df['distance'].sum()
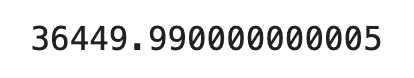
Image 5 - Total distance of the route in meters (image by author)
We’re dead on with the simple Haversine distance!
The numbers we got match the ones on Strava, so it makes sense to explore the dataset further through Python. You’ll see how to visualize the elevation profile in the next section, and we’ll compare it with the one on Strava.
How to Visualize the Elevation Profile of a Strava Route
The elevation profile shows what the name suggests - the elevation at different distances. You can use it to see where the hills are so you know how to pace your ride. We need two additional columns to visualize the elevation profile - the cumulative sum of the elevation difference, and the cumulative sum of the distance:
route_df['cum_elevation'] = route_df['elevation_diff'].cumsum()
route_df['cum_distance'] = route_df['distance'].cumsum()
route_df.head()
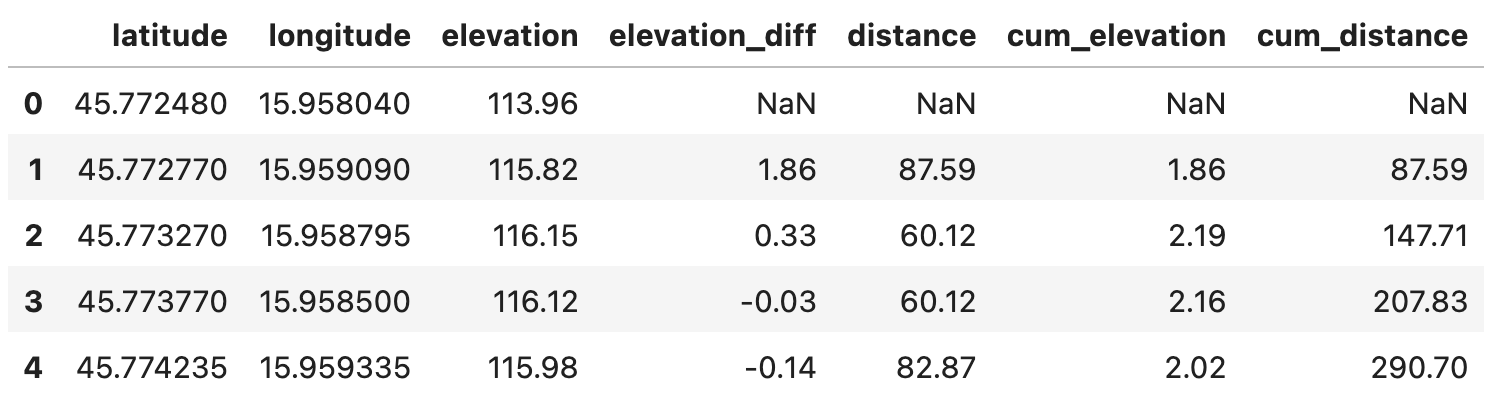
Image 6 - Cumulative sums of elevation and distance (image by author)
We need these because we want to make a line plot. The cum_distance will be on the X-axis and cum_elevation on the Y-axis. Both must be cumulative since we want to visualize the entire route, and not a single point.
Before visualization, let’s get rid of the missing values. It’s best to fill them with zeros, as that makes the most sense for this dataset:
route_df = route_df.fillna(0)
route_df.head()
Image 7 - Imputing missing values (image by author)
You’ll need this dataset in future articles, so dump it to a CSV file:
route_df.to_csv('../data/route_df_elevation_distance.csv', index=False)
Finally, we’ll use Matplotlib to visualize the elevation profile. Both distance and elevation are in meters, so keep that in mind:
plt.plot(route_df['cum_distance'], route_df['cum_elevation'], color='#101010', lw=3)
plt.title('Route elevation profile', size=20)
plt.xlabel('Distance in meters', size=14)
plt.ylabel('Elevation in meters', size=14);
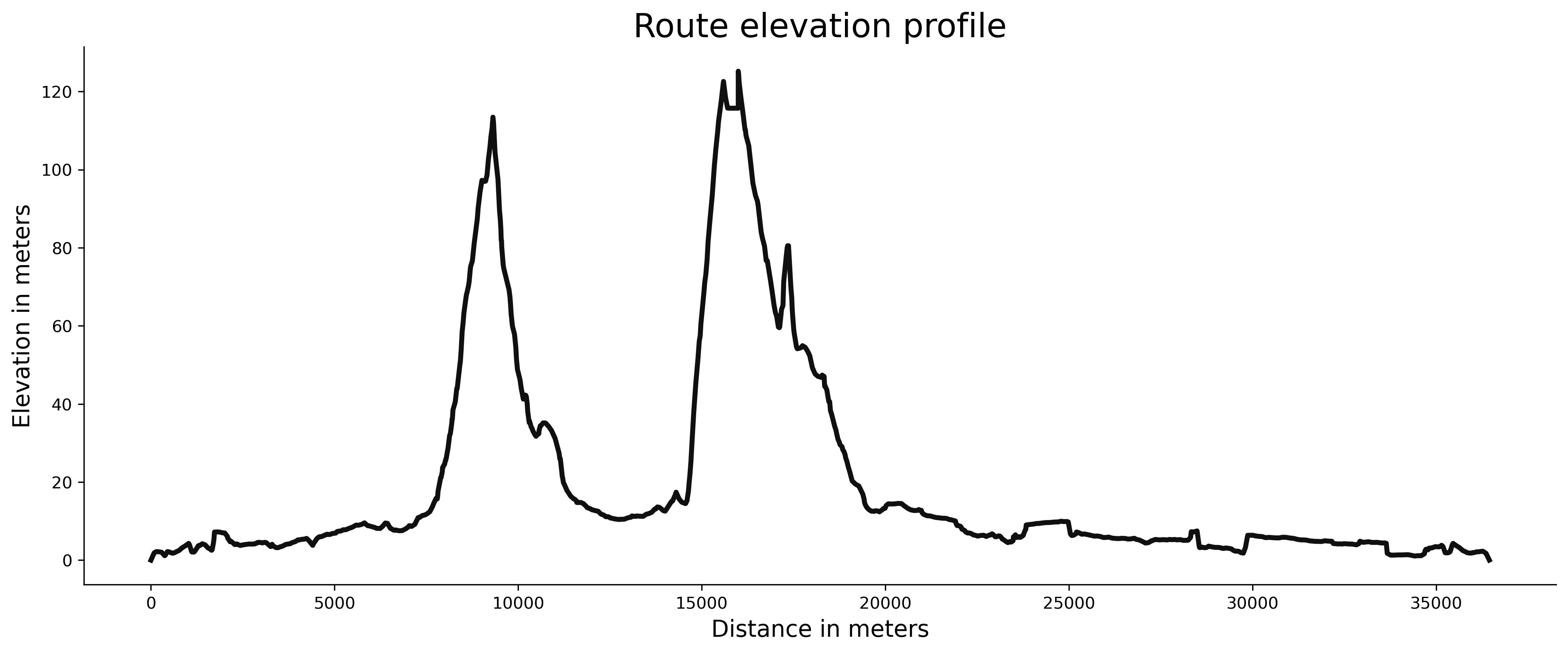
Image 8 - Route elevation profile (image by author)
There are two relatively small climbs close to one another, and the rest of the route is almost flat. Let’s compare it to the official elevation profile from Strava:
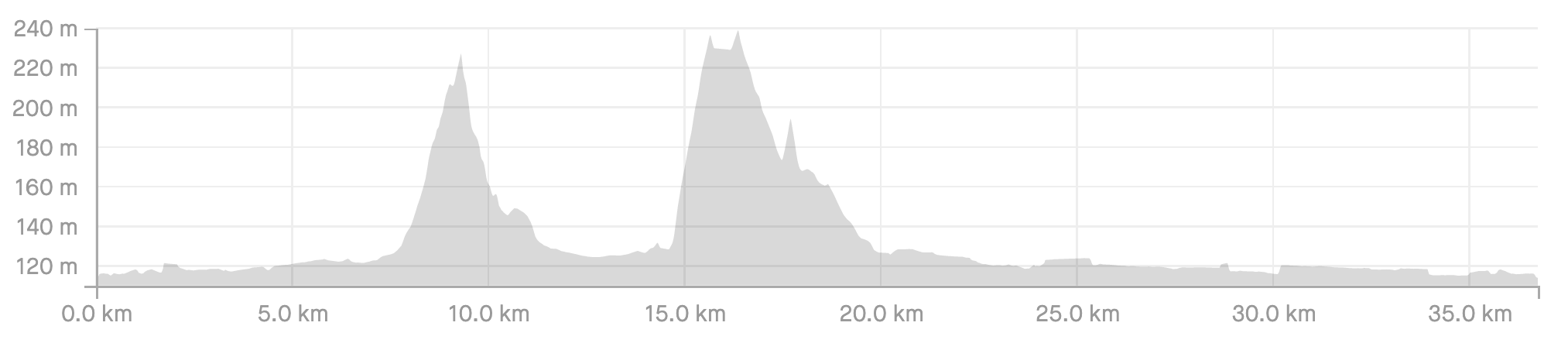
Image 9 - Route elevation profile on Strava (image by author)
Strava’s team spent more time tweaking the visuals, but the plots look close to identical! The one from Strava is wider, but that doesn’t make any real difference. Also, Strava shows the Y-axis as the elevation above the sea level, while we’re starting at zero.
Overall, we did a pretty decent job for a couple of lines of code. Let’s wrap things up next.
Conclusion
And there you have it - how to calculate the elevation difference and distance between data points, and how to visualize the elevation profile. It sounded like a lot of work at first, but Python has a library for almost anything you can imagine. These seemingly complex calculations boil down to a single function call. You’ll learn how to calculate route gradients based on elevation and distance between data points in the following article, so stay tuned.
Stay connected
- Sign up for my newsletter
- Subscribe on YouTube
- Connect on LinkedIn

