Master Machine Learning: Random Forest From Scratch With Python

Master Machine Learning: Random Forest From Scratch With Python

Machine Learning can be easy and intuitive — here’s a complete from-scratch guide to Random Forest

We already know a single decision tree can work surprisingly well. The idea of constructing a forest from individual trees seems like the natural next step.

Today you’ll learn how the Random Forest classifier works and implement it from scratch in Python. This is the sixth of many upcoming from-scratch articles, so stay tuned to the blog if you want to learn more. The links to the previous articles are located at the end of this piece.

The article is structured as follows:

  • Introduction to Random Forest
  • Math Behind Random Forest
  • From-Scratch Implementation
  • Model Evaluation
  • Comparison with Scikit-Learn
  • Conclusion

You can download the corresponding notebook here.

Introduction to Random Forest

Just like decision trees, random forests are a non-parametric model used for both regression and classification tasks. If you understood the previous article on decision trees, you’ll have no issues understanding this one.

Needless to say, but that article is also a prerequisite for this one, for obvious reasons.

The entire random forest algorithm is built on top of weak learners (decision trees), giving you the analogy of using trees to make a forest. The term “random” indicates that each decision tree is built with a random subset of data.

Here’s an excellent image comparing decision trees and random forests:

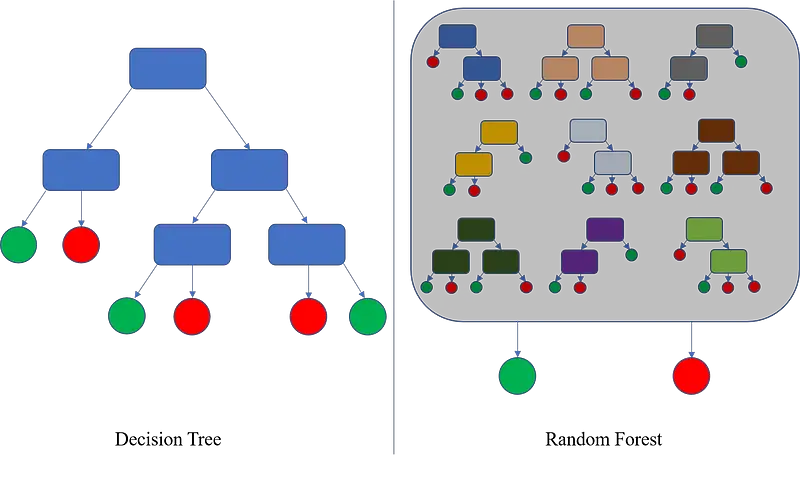
Image 1 — Decision trees vs. Random forests

Image 1 — Decision trees vs. Random forests

As simple as that.

The random forest algorithm is based on the bagging method. It represents a concept of combining learning models to increase performance (higher accuracy or some other metric).

In a nutshell:

  • N subsets are made from the original datasets
  • N decision trees are build from the subsets
  • A prediction is made with every trained tree, and a final prediction is returned as a majority vote

Here’s a diagram to drive these points home:

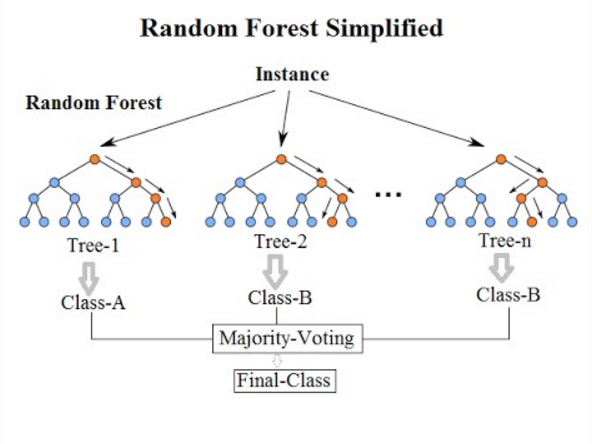
Image 2 — Random forest diagram

Image 2 — Random forest diagram

Let’s go over the math behind the algorithm next.

Math Behind Random Forest

Good news — no math today!

The math behind random forests is the same as with decision trees. You only need to implement two formulas — entropy and information gain.

If these sound like a foreign language, please refer to the previous article. Both concepts are discussed in great detail there.

The rest of the article assumes you’re familiar with the inner workings of decision trees, as it is required to build the algorithm from scratch.

From-Scratch Implementation

We’ll need three classes this time:

  1. Node - implements a single node of a decision tree
  2. DecisionTree - implements a single decision tree
  3. RandomForest - implements our ensemble algorithm

The first two classes are identical as they were in the previous article, so feel free to skip ahead if you already have them written.

Let’s start with the Node class. It is here to store the data about the feature, threshold, data going left and right, information gain, and the leaf node value. All are initially set to None. The root and decision nodes will contain values for everything besides the leaf node value, and the leaf node will contain the opposite.

Here’s the code for the class (alongside the library imports):

import numpy as np
from collections import Counter


class Node:
    '''
    Helper class which implements a single tree node.
    '''
    def __init__(self, feature=None, threshold=None, data_left=None, data_right=None, gain=None, value=None):
        self.feature = feature
        self.threshold = threshold
        self.data_left = data_left
        self.data_right = data_right
        self.gain = gain
        self.value = value

Let’s implement the decision tree classifier next. It will contain a bunch of methods, all of which are discussed below:

  • __init__() - the constructor, holds values for min_samples_split and max_depth. These are hyperparameters. The first one is used to specify a minimum number of samples required to split a node, and the second one specifies a maximum depth of a tree. Both are used in recursive functions as exit conditions
  • _entropy(s)- calculates the impurity of an input vector s
  • _information_gain(parent, left_child, right_child) calculates the information gain value of a split between a parent and two children
  • _best_split(X, y) function calculates the best splitting parameters for input features X and a target variable y. It does so by iterating over every column in X and every threshold value in every column to find the optimal split using information gain
  • _build(X, y, depth) function recursively builds a decision tree until stopping criteria is met (hyperparameters in the constructor)
  • fit(X, y) function calls the _build() function and stores the built tree to the constructor
  • _predict(x) function traverses the tree to classify a single instance
  • predict(X) function applies the _predict() function to every instance in matrix X.

Yes, it’s a lot, but you should already feel comfortable with this. Here’s the code snippet for a single decision tree:

class DecisionTree:
    '''
    Class which implements a decision tree classifier algorithm.
    '''
    def __init__(self, min_samples_split=2, max_depth=5):
        self.min_samples_split = min_samples_split
        self.max_depth = max_depth
        self.root = None
        
    @staticmethod
    def _entropy(s):
        '''
        Helper function, calculates entropy from an array of integer values.
        
        :param s: list
        :return: float, entropy value
        '''
        # Convert to integers to avoid runtime errors
        counts = np.bincount(np.array(s, dtype=np.int64))
        # Probabilities of each class label
        percentages = counts / len(s)

        # Caclulate entropy
        entropy = 0
        for pct in percentages:
            if pct > 0:
                entropy += pct * np.log2(pct)
        return -entropy
    
    def _information_gain(self, parent, left_child, right_child):
        '''
        Helper function, calculates information gain from a parent and two child nodes.
        
        :param parent: list, the parent node
        :param left_child: list, left child of a parent
        :param right_child: list, right child of a parent
        :return: float, information gain
        '''
        num_left = len(left_child) / len(parent)
        num_right = len(right_child) / len(parent)
        
        # One-liner which implements the previously discussed formula
        return self._entropy(parent) - (num_left * self._entropy(left_child) + num_right * self._entropy(right_child))
    
    def _best_split(self, X, y):
        '''
        Helper function, calculates the best split for given features and target
        
        :param X: np.array, features
        :param y: np.array or list, target
        :return: dict
        '''
        best_split = {}
        best_info_gain = -1
        n_rows, n_cols = X.shape
        
        # For every dataset feature
        for f_idx in range(n_cols):
            X_curr = X[:, f_idx]
            # For every unique value of that feature
            for threshold in np.unique(X_curr):
                # Construct a dataset and split it to the left and right parts
                # Left part includes records lower or equal to the threshold
                # Right part includes records higher than the threshold
                df = np.concatenate((X, y.reshape(1, -1).T), axis=1)
                df_left = np.array([row for row in df if row[f_idx] <= threshold])
                df_right = np.array([row for row in df if row[f_idx] > threshold])

                # Do the calculation only if there's data in both subsets
                if len(df_left) > 0 and len(df_right) > 0:
                    # Obtain the value of the target variable for subsets
                    y = df[:, -1]
                    y_left = df_left[:, -1]
                    y_right = df_right[:, -1]

                    # Caclulate the information gain and save the split parameters
                    # if the current split if better then the previous best
                    gain = self._information_gain(y, y_left, y_right)
                    if gain > best_info_gain:
                        best_split = {
                            'feature_index': f_idx,
                            'threshold': threshold,
                            'df_left': df_left,
                            'df_right': df_right,
                            'gain': gain
                        }
                        best_info_gain = gain
        return best_split
    
    def _build(self, X, y, depth=0):
        '''
        Helper recursive function, used to build a decision tree from the input data.
        
        :param X: np.array, features
        :param y: np.array or list, target
        :param depth: current depth of a tree, used as a stopping criteria
        :return: Node
        '''
        n_rows, n_cols = X.shape
        
        # Check to see if a node should be leaf node
        if n_rows >= self.min_samples_split and depth <= self.max_depth:
            # Get the best split
            best = self._best_split(X, y)
            # If the split isn't pure
            if best['gain'] > 0:
                # Build a tree on the left
                left = self._build(
                    X=best['df_left'][:, :-1], 
                    y=best['df_left'][:, -1], 
                    depth=depth + 1
                )
                right = self._build(
                    X=best['df_right'][:, :-1], 
                    y=best['df_right'][:, -1], 
                    depth=depth + 1
                )
                return Node(
                    feature=best['feature_index'], 
                    threshold=best['threshold'], 
                    data_left=left, 
                    data_right=right, 
                    gain=best['gain']
                )
        # Leaf node - value is the most common target value 
        return Node(
            value=Counter(y).most_common(1)[0][0]
        )
    
    def fit(self, X, y):
        '''
        Function used to train a decision tree classifier model.
        
        :param X: np.array, features
        :param y: np.array or list, target
        :return: None
        '''
        # Call a recursive function to build the tree
        self.root = self._build(X, y)
        
    def _predict(self, x, tree):
        '''
        Helper recursive function, used to predict a single instance (tree traversal).
        
        :param x: single observation
        :param tree: built tree
        :return: float, predicted class
        '''
        # Leaf node
        if tree.value != None:
            return tree.value
        feature_value = x[tree.feature]
        
        # Go to the left
        if feature_value <= tree.threshold:
            return self._predict(x=x, tree=tree.data_left)
        
        # Go to the right
        if feature_value > tree.threshold:
            return self._predict(x=x, tree=tree.data_right)
        
    def predict(self, X):
        '''
        Function used to classify new instances.
        
        :param X: np.array, features
        :return: np.array, predicted classes
        '''
        # Call the _predict() function for every observation
        return [self._predict(x, self.root) for x in X]

Finally, let’s build the forest. This class is built on top of a single decision tree and has the following methods:

  • __init__() - the constructor, holds hyperparameter values for the number of trees in the forest, minimum samples split, and maximum depth. It will also hold individually trained decision trees once the model is trained
  • _sample(X, y) function applies bootstrap sampling to input features and input target
  • fit(X, y) function trains the classifier model
  • predict(X) function makes predictions with individual decision trees and then applies majority voting for the final prediction

Code-wise it’s a much simpler class than a decision tree. Here’s the entire snippet:

class RandomForest:
    '''
    A class that implements Random Forest algorithm from scratch.
    '''
    def __init__(self, num_trees=25, min_samples_split=2, max_depth=5):
        self.num_trees = num_trees
        self.min_samples_split = min_samples_split
        self.max_depth = max_depth
        # Will store individually trained decision trees
        self.decision_trees = []
        
    @staticmethod
    def _sample(X, y):
        '''
        Helper function used for boostrap sampling.
        
        :param X: np.array, features
        :param y: np.array, target
        :return: tuple (sample of features, sample of target)
        '''
        n_rows, n_cols = X.shape
        # Sample with replacement
        samples = np.random.choice(a=n_rows, size=n_rows, replace=True)
        return X[samples], y[samples]
        
    def fit(self, X, y):
        '''
        Trains a Random Forest classifier.
        
        :param X: np.array, features
        :param y: np.array, target
        :return: None
        '''
        # Reset
        if len(self.decision_trees) > 0:
            self.decision_trees = []
            
        # Build each tree of the forest
        num_built = 0
        while num_built < self.num_trees:
            try:
                clf = DecisionTree(
                    min_samples_split=self.min_samples_split,
                    max_depth=self.max_depth
                )
                # Obtain data sample
                _X, _y = self._sample(X, y)
                # Train
                clf.fit(_X, _y)
                # Save the classifier
                self.decision_trees.append(clf)
                num_built += 1
            except Exception as e:
                continue
    
    def predict(self, X):
        '''
        Predicts class labels for new data instances.
        
        :param X: np.array, new instances to predict
        :return: 
        '''
        # Make predictions with every tree in the forest
        y = []
        for tree in self.decision_trees:
            y.append(tree.predict(X))
        
        # Reshape so we can find the most common value
        y = np.swapaxes(a=y, axis1=0, axis2=1)
        
        # Use majority voting for the final prediction
        predictions = []
        for preds in y:
            counter = Counter(x)
            predictions.append(counter.most_common(1)[0][0])
        return predictions

You might not understand everything fully in one sitting, but this won’t be too much of a challenge if you understood decision trees.

Let’s train and evaluate our model next.

Model Evaluation

Let’s test our classifier next. We’ll use the Iris dataset from Scikit-Learn. The following code snippet loads the dataset and separates it into features (X) and the target (y):

from sklearn.datasets import load_iris

iris = load_iris()

X = iris['data']
y = iris['target']

Let’s split the dataset into training and testing portions next. The following code snippet does just that, in an 80:20 ratio:

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

And now let’s do the training. The code snippet below trains the model with default hyperparameters and makes predictions on the test set:

model = RandomForest()
model.fit(X_train, y_train)
preds = model.predict(X_test)

Let’s take a look at the generated predictions (preds):

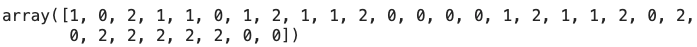
Image 3 — Custom random forest predictions on the test set (image by author)

Image 3 — Custom random forest predictions on the test set (image by author)

And now at the actual class labels (y_test):

Image 4 — Test set class labels (image by author)

Image 4 — Test set class labels (image by author)

As you can see, both are identical, indicating a perfectly accurate classifier. You can further evaluate the performance if you want. The code below prints the accuracy score on the test set:

from sklearn.metrics import accuracy_score

accuracy_score(y_test, preds)

If you were to run the above code, the value of 1.0 would get printed, indicating a perfect classifier. The Iris dataset is incredibly easy to classify correctly, so don’t let this fool you.

Let’s compare our classifier to the one built into Scikit-Learn next.

Comparison with Scikit-Learn

We want to know if our model is any good, so let’s compare it with something we know works well — a RandomForestClassifier class from Scikit-Learn.

You can use the following snippet to import the model class, train the model, make predictions, and print the accuracy score:

from sklearn.ensemble import RandomForestClassifier

sk_model = RandomForestClassifier()
sk_model.fit(X_train, y_train)
sk_preds = sk_model.predict(X_test)

accuracy_score(y_test, sk_preds)

As you would expect, we get a perfect accuracy score of 1.0.

And that’s all for today. Let’s wrap things up in the next section.

Conclusion

And there you have it — how to build a forest from the trees. It’s easier than you would think, especially if you consider that random forests are among the top-performing machine learning algorithms today.

You now know how to implement the Decision tree classifier algorithm from scratch. Does that mean you should ditch the de facto standard machine learning libraries? No, not at all. Let me elaborate.

Just because you can write something from scratch doesn’t mean you should. Still, knowing every detail of how algorithms work is a valuable skill and can help you stand out from every other fit and predict data scientist.

Thanks for reading, and please stay tuned to the blog if you’re interested in more machine learning from scratch articles.

Stay connected