Significantly improving your models doesn’t take much time — Here’s how to get started
Tuning neural network models is no joke. There are so many hyperparameters to tune, and tuning all of them at once using a grid search approach could take weeks, even months. Learning rate is a hyperparameter you can tune in a couple of minutes, provided you know how. This article will teach you how.
The learning rate controls how much the weights are updated according to the estimated error. Choose too small of a value and your model will train forever and likely get stuck. Opt for a too large learning rate and your model might skip the optimal set of weights during training.
You’ll need TensorFlow 2+, Numpy, Pandas, Matplotlib, and Scikit-Learn installed to follow along.
Don’t feel like reading? Watch my video instead:
You can download the source code on GitHub.
Dataset used and data preprocessing
I don’t plan to spend much time here. We’ll use the same dataset as in the previous article— the wine quality dataset from Kaggle:
Image 1 — Wine quality dataset from Kaggle (image by author)
You can use the following code to import it to Python and print a random couple of rows:
import os
import numpy as np
import pandas as pd
import warnings
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
warnings.filterwarnings('ignore')
df = pd.read_csv('data/winequalityN.csv')
df.sample(5)
We’re ignoring the warnings and changing the default TensorFlow log level just so we don’t get overwhelmed with the output.
Here’s how the dataset looks like:

Image 2 — A random sample of the wine quality dataset (image by author)
The dataset is mostly clean, but isn’t designed for binary classification by default (good/bad wine). Instead, the wines are rated on a scale. We’ll address that now, with a bunch of other things:
- Delete missing values— There’s only a handful of them so we won’t waste time on imputation.
- Handle categorical features— The only one is
type, indicating whether the wine is white or red. - Convert to a binary classification task— We’ll declare any wine with a grade of 6 and above as good, and anything below as bad.
- Train/test split— A classic 80:20 split.
- Scale the data— The scale between predictors differs significantly, so we’ll use the
StandardScalerto bring the values closer.
Here’s the entire data preprocessing code snippet:
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
# Prepare the data
df = df.dropna()
df['is_white_wine'] = [
1 if typ == 'white' else 0 for typ in df['type']
]
df['is_good_wine'] = [
1 if quality >= 6 else 0 for quality in df['quality']
]
df.drop(['type', 'quality'], axis=1, inplace=True)
# Train/test split
X = df.drop('is_good_wine', axis=1)
y = df['is_good_wine']
X_train, X_test, y_train, y_test = train_test_split(
X, y,
test_size=0.2, random_state=42
)
# Scaling
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
And here’s how the first couple of scaled rows look like:

Image 3 — Scaled training set (image by author)
Once again, please refer to the previous article if you want more detailed insights into the logic behind data preprocessing.
With that out of the way, let’s see how to optimize the learning rate.
How to optimize learning rate in TensorFlow
Optimizing the learning rate is easy once you get the gist of it. The idea is to start small — let’s say with 0.001 and increase the value every epoch. You’ll get terrible accuracy when training the model, but that’s expected. Don’t even mind it, as we’re only interested in how the loss changes as we change the learning rate.
Let’s start by importing TensorFlow and setting the seed so you can reproduce the results:
import tensorflow as tf
tf.random.set_seed(42)
We’ll train the model for 100 epochs to test 100 different loss/learning rate combinations. Here’s the range for the learning rate values:

Image 4 — Range of learning rate values (image by author)
A learning rate of 0.001 is the default one for, let’s say, Adam optimizer, and 2.15 is definitely too large.
Next, let’s define a neural network model architecture, compile the model, and train it. The only new thing here is the LearningRateScheduler. It allows us to enter the above-declared way to change the learning rate as a lambda function.
Here’s the entire code:
initial_model = tf.keras.Sequential([
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dense(256, activation='relu'),
tf.keras.layers.Dense(256, activation='relu'),
tf.keras.layers.Dense(1, activation='sigmoid')
])
initial_model.compile(
loss=tf.keras.losses.binary_crossentropy,
optimizer=tf.keras.optimizers.Adam(),
metrics=[
tf.keras.metrics.BinaryAccuracy(name='accuracy')
]
)
initial_history = initial_model.fit(
X_train_scaled,
y_train,
epochs=100,
callbacks=[
tf.keras.callbacks.LearningRateScheduler(
lambda epoch: 1e-3 * 10 ** (epoch / 30)
)
]
)
The training will start now and you’ll see a decent accuracy immediately — around 75% — but it will drop after 50-something epochs because the learning rate became too large. After 100 epochs, the initial_model had around 60% accuracy:

Image 5 — Initial model training log (image by author)
The initial_history variable now has information on loss, accuracy, and learning rate. Let’s plot all of them:
import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams['figure.figsize'] = (18, 8)
rcParams['axes.spines.top'] = False
rcParams['axes.spines.right'] = False
plt.plot(
np.arange(1, 101),
initial_history.history['loss'],
label='Loss', lw=3
)
plt.plot(
np.arange(1, 101),
initial_history.history['accuracy'],
label='Accuracy', lw=3
)
plt.plot(
np.arange(1, 101),
initial_history.history['lr'],
label='Learning rate', color='#000', lw=3, linestyle='--'
)
plt.title('Evaluation metrics', size=20)
plt.xlabel('Epoch', size=14)
plt.legend();
Here’s the chart:
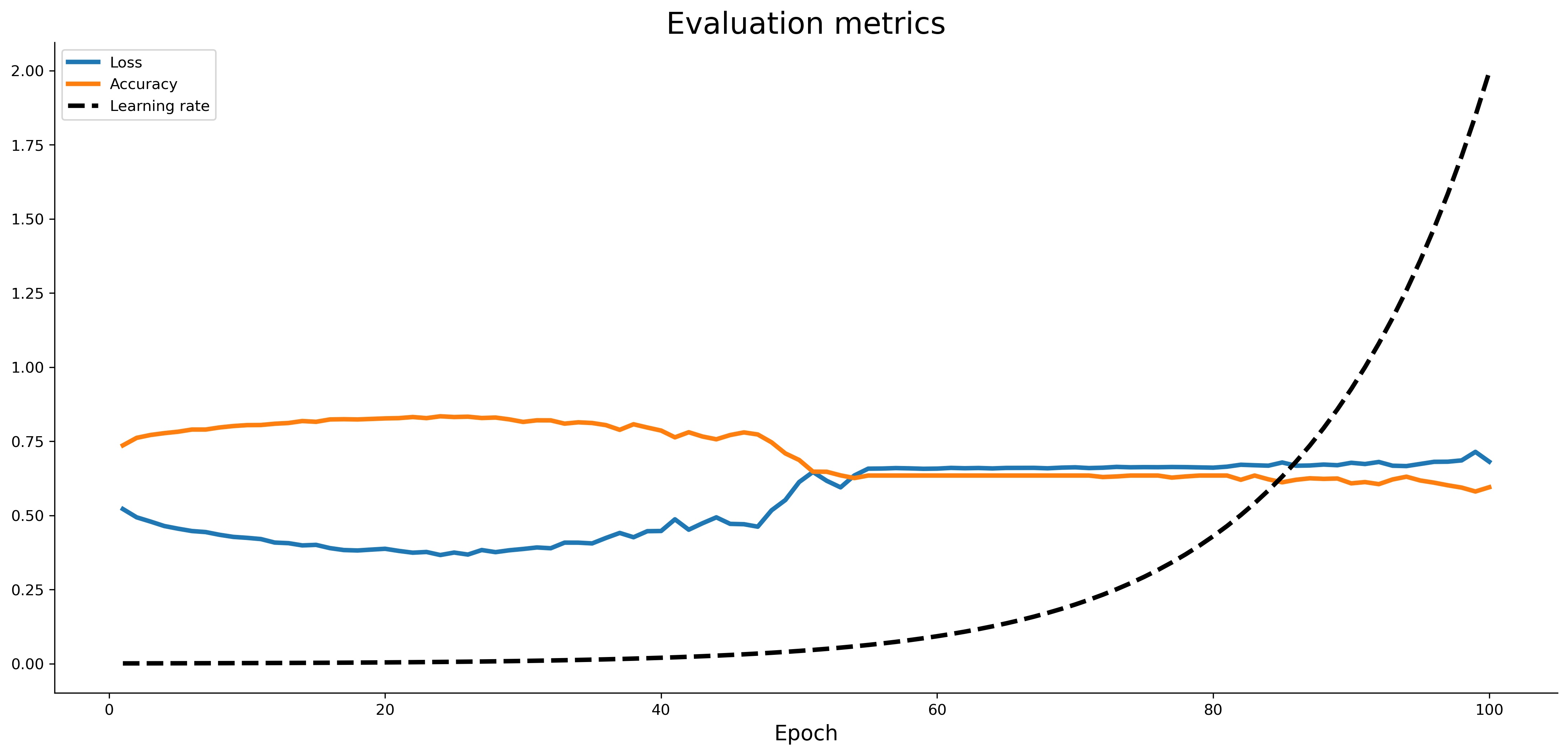
Image 6 — Loss vs. accuracy vs. learning rate (image by author)
The accuracy dipped significantly around epoch 50 and flattened for a while, before starting to dip further. The exact opposite happened to loss, which makes sense.
You can now plot the loss against learning rate on a logarithmic scale to eyeball where the minimum loss was achieved:
learning_rates = 1e-3 * (10 ** (np.arange(100) / 30))
plt.semilogx(
learning_rates,
initial_history.history['loss'],
lw=3, color='#000'
)
plt.title('Learning rate vs. loss', size=20)
plt.xlabel('Learning rate', size=14)
plt.ylabel('Loss', size=14);
Here’s the chart:
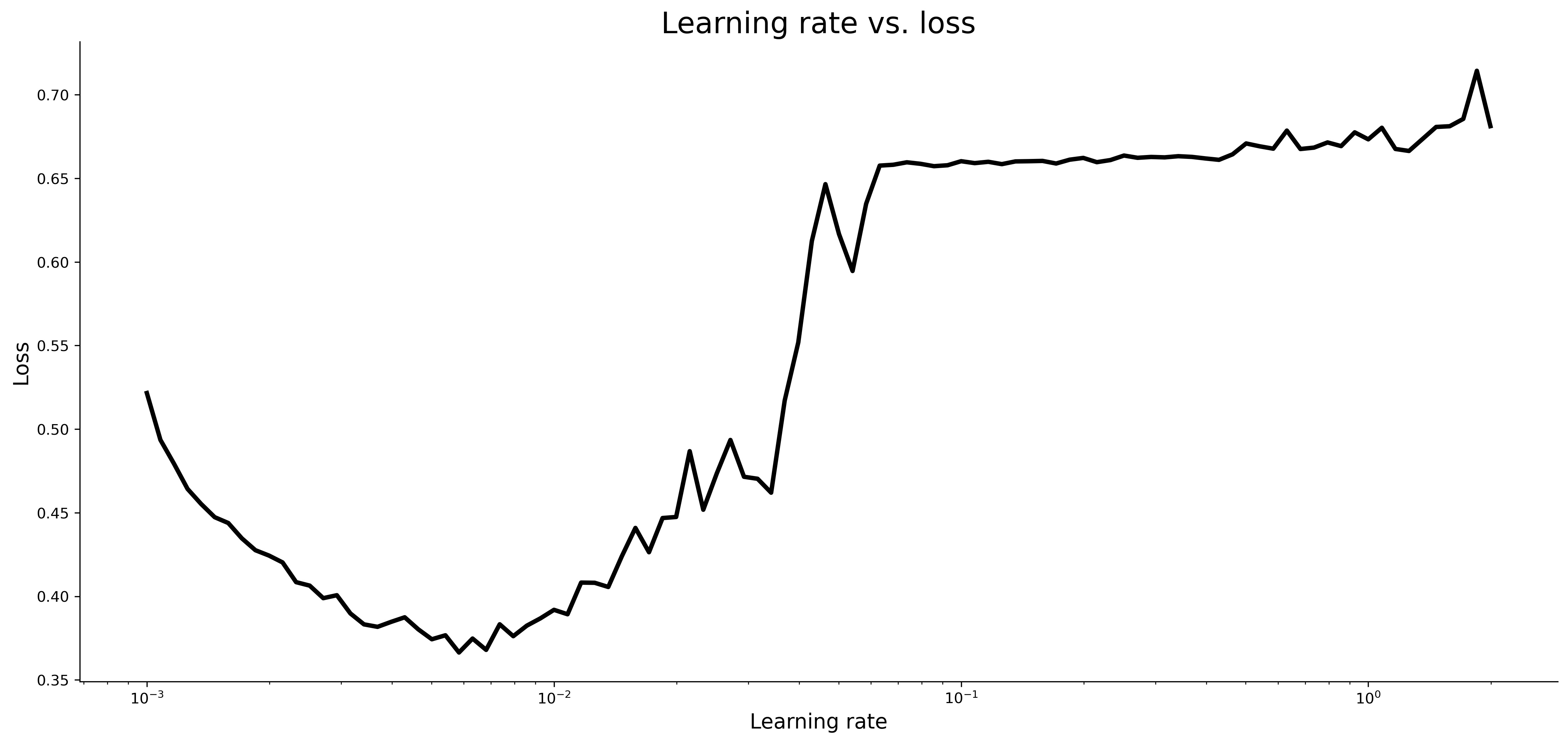
Image 7 — Learning rate vs. loss (image by author)
You’ll generally want to select a learning rate that achieves the lowest loss, provided that the values around it aren’t too volatile. Keep in mind that the X-axis is on a logarithmic scale. The optimal learning rate is around 0.007:
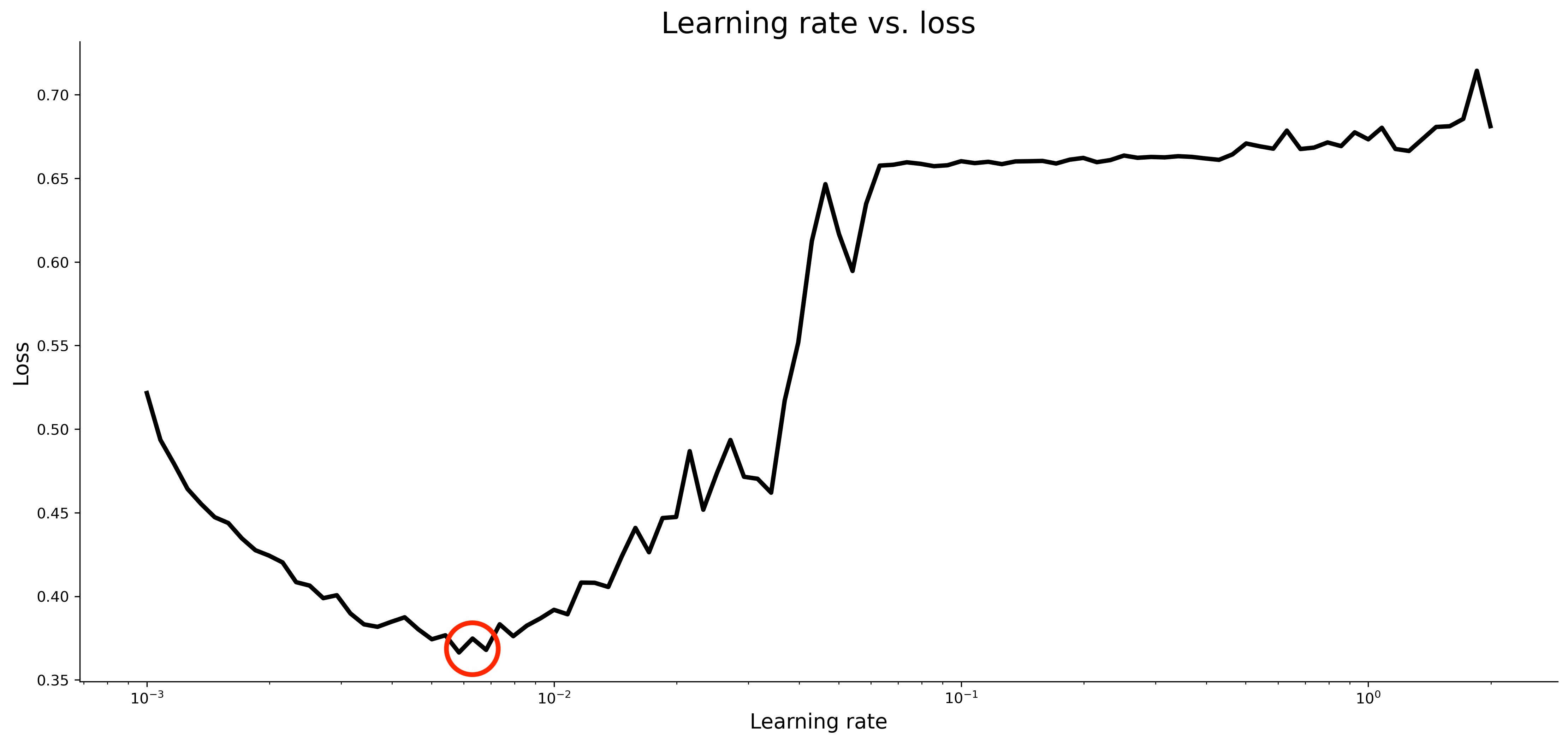
Image 8 — Optimal learning rate (image by author)
So let’s train a model with a supposedly optimal learning rate and see if we can outperform the default one.
Train a model with optimal learning rate
With a learning rate of 0.007 in mind, let’s write another neural network model. You won’t need the LearningRateScheduler this time:
model_optimized = tf.keras.Sequential([
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dense(256, activation='relu'),
tf.keras.layers.Dense(256, activation='relu'),
tf.keras.layers.Dense(1, activation='sigmoid')
])
model_optimized.compile(
loss=tf.keras.losses.binary_crossentropy,
optimizer=tf.keras.optimizers.Adam(learning_rate=0.007),
metrics=[
tf.keras.metrics.BinaryAccuracy(name='accuracy')
]
)
history_optimized = model_optimized.fit(
X_train_scaled,
y_train,
epochs=100
)
We got 76% accuracy with the default learning rate in the previous article, so it’ll be interesting to see if learning rate optimization can increase it. The reported accuracy on the train set looks too good to be true, so it’s likely our model is overfitting:

Image 9 — Optimized model training log (image by author)
It won’t matter too much if we’ve managed to increase the performance on the test set, but you could save yourself some time by training the model for fewer epochs.
Here’s how the accuracy vs. loss looks like for the optimized model:
plt.plot(
np.arange(1, 101),
history_optimized.history['loss'],
label='Loss', lw=3
)
plt.plot(
np.arange(1, 101),
history_optimized.history['accuracy'],
label='Accuracy', lw=3
)
plt.title('Accuracy vs. Loss per epoch', size=20)
plt.xlabel('Epoch', size=14)
plt.legend()
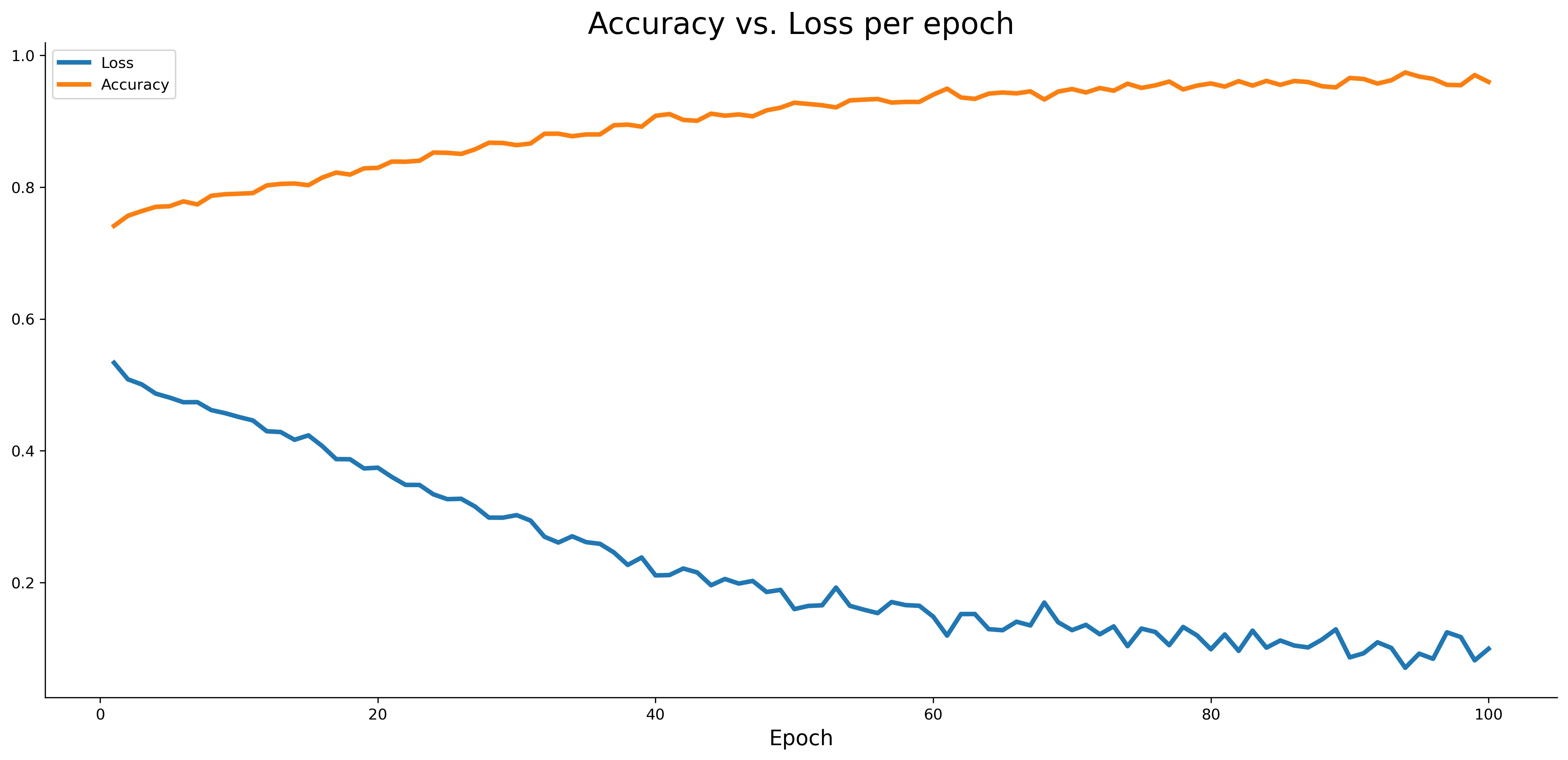
Image 10 — Accuracy vs loss on the training set (image by author)
Let’s finally calculate the predictions and evaluate them against the test set. Here’s the code:
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score
predictions = model_optimized.predict(X_test_scaled)
prediction_classes = [1 if prob > 0.5 else 0 for prob in np.ravel(predictions)]
print(f'Accuracy on the test set:
{accuracy_score(y_test, prediction_classes):.2f}')
print()
print('Confusion matrix:')
print(confusion_matrix(y_test, prediction_classes))
And here’s the output:

Image 11 — Test set evaluation metrics (image by author)
To summarize, optimizing the learning rate alone managed to increase the model accuracy by 3% on the test set. It might not sound huge, but it’s an excellent trade-off for the amount of time it took. Moreover, it’s only the first of many optimizations you can do to a neural network model, and it’s one less hyperparameter you need to worry about.
Stay tuned to learn how to optimize a neural network architecture — the post will be up in a couple of days. Thanks for reading!
Stay connected
- Sign up for my newsletter
- Subscribe on YouTube
- Connect on LinkedIn

